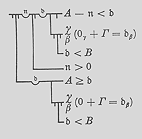 Frege's Begriffsschrift
home
Frege's Begriffsschrift
homeLogicism and logical empirism
This little piece is inspired by the brilliant article (Musgrave 1977). Alan Musgrave investigates what he calls a "historical riddle", namely that in some sense "logicism" was already refuted when it became the basis of "logical empirism" (which goes also by the name "Neopositivism" and which was championed by the Vienna Circle). By "logicism" we mean roughly the idea that all of mathematics can be reduced to "logic" (as always the story is more complicated: we take logicism to claim at least that (i) all mathematical concepts can be defined in terms of logical concepts and that (ii) all mathematical theorems can be deduced from basic logical truth. See Reck (undated, p.22) for a more detailed treatment.).
From Kant via Frege to Carnap
The philosophy of the Vienna Circle was radically anti-metaphysical. The main doctrine was that only empirical or logical statements constitute the source of reliable knowledge. Kant's infamous synthetic a priori judgments were denied, in favor of synthetic a posteriori (i.e. empirical) and "logical statements" which, using Kant's terminology, may be identified with analytic a priori judgments (since "analytic" judgments are independent of any experience by definition, the add on "a priori" is actually superfluous.). Now, what is the place for mathematics (and its alleged logical foundation) in this debate? For Kant mathematics was the prime example for a synthetic a priori truth. Indeed, e.g. geometry seemed to provide certain knowledge about the world - independent of experience (i.e. a priori). Agreed, given the discovery of non-Euclidean geometries in the 19th century and especially the fact that the world we are living in seems to be ruled by such a non-Euclidean geometry, weakens this claim. However, it remains evident that the truth of a mathematical theorem (say, that there are infinite many primes) is by no way founded empirically. Hence, according to the logical empirists, only the other class of acceptable statements is available and mathematics needs to be essentially of an analytical i.e. logical kind. That was exactly the view Carnap held:"(...) I gained the conviction that knowledge in mathematics is analytic in the general sense that it has essentially the same nature as knowledge of logic." (Carnap 1963, p.12)The reason for this conviction was certainly the alleged success of the logicism to ground all of mathematics on logical notions only, as started by Gottlob Frege and carried further by Russell and Whitehead in their Principia Mathematica.
However, and that is the puzzling situation Musgrave calls the "historical riddle", this idea became one of the cornerstones of the logical empirism since the 20s when the unfeasibility of logicism was apparent aldready. And even more puzzling:
"And yet logical empiricists did not ignore the difficulties which beset the logicist programme - indeed, they were better aware of them than most. This then, is my historical riddle." (Mussgrave, 1977, p.100)Musgrave's bottom line is that the "logicism" which survived into logical empirism was different in character that the original version. The new version he calls "if-thenism" (an odd labeling, due to Putnam. Its meaning will become clear in the following). According to Musgrave this if-thenism is not only a much weaker thesis than the original logicism but still refutable. However, the rhetoric of old-style logicism remained and was "used as a stick to beat philosophical opponents" (Musgrave, p.113). But we are getting ahead of the story. In the next section the fall of the logicist program will be addressed.
The fall of Logicism proper
It is well known that Frege's attempt to base arithmetics on logic suffered from the logical paradoxes (e.g. Russel's antinomy). He used the so-called "unrestricted set abstraction" which states that there is for every property which is described via an open formula a set of things which possess this property. To avoid the problem one needs to modify the theory, e.g. Russell came up with his "theory of types". However, as Musgrave puts it sarcastically,
"Unfortunately Russel's new logic, as well as preventing the deduction of paradoxes, also prevented the deduction of mathematics. Russell therefore supplemented it with additional axioms, the Axiom of Infinity, Choice, and Reducibility (...)" (Musgrave, 1977, p.102)The "theory of types" together with these axioms is indeed powerful enough to obtain classical mathematics from it.
The other (and more widespread) solution was provided by Zermelo's axiomatization of set theory which restricted the set abstraction. Again, this set theory together with logic was powerful enough to yield mathematics, but not so powerful as to yield contradictions. However, as long as one does not count set theory as logic (and Musgrave p.102-108 argues that one ought not) one has not reduced mathematics to logic but to a specific branch of mathematics only. And the situation is the same with the axioms Russell needed to introduce. They also have a "non-logical" character. Musgrave quotes Kneale and Kneale (1962):
"There is something profoundly unsatisfactory about the axiom of infinity. It cannot be described as a truth of logic in any reasonable use of the term and so the introduction of it as a primitive proposition amounts in effect to the abandonment of Frege'S project of exhibiting arithmetics as a development of logic."This was even recognized by Russell himself (quoted from Musgrave p. 108):
"I wanted certainty in the kind of way in which people want religious faith. I thought that certainty is more likely to be found in mathematics than elsewhere. (...) But as the work proceeded, I was continually reminded of the fable about the elephant and the tortoise. Having constructed an elephant upon which the mathematical world could rest, I found the elephant tottering, and proceeded to construct a tortoise to keep the elephant from falling. But the tortoise was no more secure than the elephant, and after some twenty years of very arduous toil, I came to the conclusion that there was nothing more that I could do in the way of making mathematical knowledge indubitable. Then came the First World War, and my thoughts became concentrated on human misery and folly."
The if-thenist maneuver
Now, how to rescue logicism from defeat in a situation like this? According to Musgrave it was again Russell who found a way to rescue at least parts of the original program (however, as the above quote shows, not even to his own complete satisfaction). As explained above one has to dispense with the idea that all primitive concepts of mathematics can be described in logical terms, i.e. there are genuine mathematical axioms. But the distinguished position of logic remains the following: given the axioms (mathematical and logical) all true mathematical theorems can be derived logically from them. Now we are in the position to understand the term if-thenism: it refers to the conditional structure of any if sentence. Mathematical statements are viewed as conditionals linking a set of axioms with a theorem. Musgrave emphasizes that this is not a trivial claim, since"(...) what it says is that all mathematical proofs can be formalized."However, one should note that it applies only to axiomatized portions of mathematics. Given that mathematics is a creative enterprise which does certainly not start with an axiomatic system this account seems to be defective.
However, what really destroys if-thenism are Gödel's incompleteness theorems from 1931. Musgrave claims that the original logicism tacitly assumed that arithmetic truth and provability can be identified and that this thesis was carried over into if-thenism.
"They claimed, in other words, that all arithmetic truths could be formally proved from arithmetic axioms, so that the conditionals linking the two could be formally proved from logical axioms alone. Hence if-thenism, while it was not refuted by the earlier discovery of the paradoxes, seems to have been refuted at about the time it was proposed by Gödel's first incompleteness theorem." (Musgrave, p.124)Any "post-Gödelian if-thenism" needs so much distortion from its original thesis that Musgrave is led to the conclusion, that
"(...) we will have to admit that the question of the epistemological status of mathematics remains open."I think that these are good closing words.