Indeterminism in classical physics
Logo A paradigmatic example for a causal system
home


Indeterminism (and acausality) in classical physics

Contrary to popular belief classical physics is not deterministic and even allows for systems in which things happen without a cause (the relation between "causality" and "determinism" is subtle, see e.g. "Causality and Determinism: Tension, or Outright Conflict?" by Carl Hoefer.). In any event, for the moment we take "causality" to mean, that every event has a cause. Determinism is roughly the idea, that the "state" at a given time determines the future uniquely, i.e. indeterminism could be described as "a single past can be followed by many futures".

Niceties aside, most people would assume that Newton's mechanics is deterministic (and that the state in the past could be conceived somehow as "causal" influence). However, there are interesting counter examples!

Supertasks

A supertask is a task which occurs within a finite interval of time but involves infinitely many steps. Earman (1996) contains a detailed discussion of supertasks and their philosophical implications. We only want to focus on a particular neat example by Laraudogoitia. In 1996 he has invented a particular simple "physical" realization of such a supertask in which an infinite collection of equal masses is located at positions 1/2, 1/4, 1/8, 1/16 ... along a line of unit length. He now introduces a particle of the same mass and unit velocity (i.e. unitlength/second) directed along the line which performs an elastic collision with the first particle on the line (at 1/2). It will transfer its momentum and this collisions continue for all the infinite masses along the line.

Logo

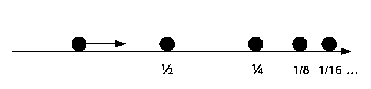
However, the amount of time is finite, since the distances decrease accordingly. In our example with unit-length and unit-velocity the collisions will be over after 1 second. But given that there is no "last" particle in the chain, there is no particle leaving the system. Momentum and energy conservation are violated. An other way to illustrate this point is by noting that for all times t>1 each mass has performed its collision already and is at rest at the position of its former neighbor, hence kinetic energy and momentum are lost. But what is the relation to indeterminism? Apply the following powerful argument: Newton's mechanics is invariant under time reversal and this transformation takes the supertask described above to a situation in which a particle is set into spontaneous motion. Such a "self-excitation" does surly compromise determinism.

Agreed, this example appears contrived or at least unphysical. There is no infinite number of particles in the world and in order to achieve a constant mass for each particle one needs to constantly increase their mass-density (given that they have a decreasing amount of space to occupy). However, many derivations in physics actually involve hand waving infinity-arguments, e.g. if you introduce field theory as a limit process from a chain of oscillators. This shows that one can not simply meet the supertask-challenge by dismissing infinities as "unphysical" from the outset (see Earman (1996) for more details and Norton (1999) for a quantum mechanical generalization). But should we conclude that these features are just artefacts from dealing with infinite-systems? The next example of indeterminism in classical mechanics does refute this hope:

Norton's dome

John Norton from Pittsburgh has developed an ingenious example of a failure of causality in classical mechanics: the dome (Norton 2003, 2006). Due to the special shape of the dome it admits solutions where a point like unit mass begins to slide down from the top without any cause that has set the mass in motion. 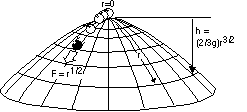Logo The shape of the dome is defined by the relation h=(2/3g)r**(3/2), with r the radial coordinate and h the vertical distance towards the top of the dome. This leads to the equation-of-motion d**2r/dt**2=(r)**(1/2). The initial conditions are r(t)=dr/dt=0. Besides the trivial solution, r(t)=0, this allows also for the solution: r(t)=1/144(t-T)**4 (for t>T), with T a free parameter (with the dimension of time). After the time T has elapsed, the body slides down the top spontaneously! Check out for yourself that the equation-of-motion is indeed correct and that the non-trivial solution solves it.

In Norton (2006) he replies to common criticism and Malament (2006) contains a critical examination of the alleged indeterminism. To all appearances we have here an occurrence of indeterministic (and acausal) behavior in Newton's physics! In Norton (2003) this example is utilized to strengthen the claim that "causality" is not fundamental, but merely "folk science".

References

Other internet resources